 Ilya
Ilya
кстати так и не понял на курсе матана, чем отображение обобщает термин "функция"
да одно и то же, просто применяется в разных контекстах
 Евгений
Евгений
Например рассотрим f: R -> R, но f=1/x. Тогда в 0 f не определена, т. е правильно f : R -> Maybe R. И f(0) = Nothing
 Ilya
Ilya
Например рассотрим f: R -> R, но f=1/x. Тогда в 0 f не определена, т. е правильно f : R -> Maybe R. И f(0) = Nothing
блин, это очень неаккуратно. можно неправильно понять
 Влод
Влод
Вы это осторожнее с Nothing, т.к. мейби это решение для перевода частичной функции в полную, т.е. захват сайд эффекта функции
 Влод
Влод
Всмысле, a -> Maybe b превращает частичную функцию a -> в нормальную. Частичная значит "не для всех а определено значение функции". Характерный пример -- любая частично-рекурсивная функция, не являющаяся тотальной
 Влод
Влод
Например рассотрим f: R -> R, но f=1/x. Тогда в 0 f не определена, т. е правильно f : R -> Maybe R. И f(0) = Nothing
 Евгений
Евгений
"f: R -> R, f(x) = 1/x" абсолютно корректная запись с точки зрения математики, если что
Ну разве что со стороны школьной математики. Со стороны даже обычной университетской правильно f: (-inf, 0) union (0, +inf) -> R
Ну или f: R -> R union {inf}
 Ilya
Ilya
 Влод
Влод
ну это чушь, конечно же
Поосторожнее с такими словами) у меня с подобной фразы уже второй день как горит
 Ilya
Ilya
Поосторожнее с такими словами) у меня с подобной фразы уже второй день как горит
ты очень чувствительный человек, если у тебя горит даже когда её пишут не тебе:)
 Евгений
Евгений
думаю, ты слышал про область определения? функций, операторов
Функция X->Y это подмножество F множества 2^XxY, такое что:
1. для любого x:X существует y:Y, т.ч (x, y) in F
2. для любых (x, y1): F и (x, y2): F y1=y2
 Ilya
Ilya
Так написано у Бурбаки => истина в конечной инстанции
ну после таких формулировок что-то обсуждать уже не хочется:)
 Ilya
Ilya
мы можем написать f : R -> R, но D(f) = R \ {0}
а обычный рабочий математик понимает такую запись вполне нормально. и понимает, зачем так писать.
 Евгений
Евгений
ну после таких формулировок что-то обсуждать уже не хочется:)
А чего обсуждать? Общепринятые определения, выдвинутые великой школой математиков?
Тем более, что после них в фаундейшонсках классической математики ничего не произошло вообще
 Влод
Влод
а обычный рабочий математик понимает такую запись вполне нормально. и понимает, зачем так писать.
У Колмогорова просто функции с сайд эффектами
 Мерль
Мерль
Например у нас есть функция, которая возвращает сумму случайного числа и аргумента
Он может быть определена на всём множестве рациональных чисел, например.
Но её результат зависит не только от аргумента.
Или функция, вон та самая фунция 1/x
Она определена не на всём множестве аргументов, но тем не менее результат её выполнения зависит только от аргумента, принадлежащего области области определения.
 Ilya
Ilya
А чего обсуждать? Общепринятые определения, выдвинутые великой школой математиков?
Тем более, что после них в фаундейшонсках классической математики ничего не произошло вообще
а можно уважаемого бурбакиста попросить прокомментировать подобную нотацию?
 Евгений
Евгений
а обычный рабочий математик понимает такую запись вполне нормально. и понимает, зачем так писать.
Как говорил нам в университете товарищ Вавилов чтобы правильно пользоваться некорректными формулировками необходимо сначала освоить корректные
 Мерль
Мерль
На двух соседних кафедрах нотации могут отличаться
Предлагаю ещё о порядке индексов матриц посраться
Тоже благодатная тема
 Ilya
Ilya
Как говорил нам в университете товарищ Вавилов чтобы правильно пользоваться некорректными формулировками необходимо сначала освоить корректные
не вижу, где я давал повода усомниться в том, что я понимаю классическое определение функции =)
 Евгений
Евгений
Ну то есть ремесло это хорошо, правильно и круто. Но типа не надо путать ремесло и формализм
 Евгений
Евгений
Если у тебя разойдётся функция в одной точке, дажё и не разрушая её голоморфность, для остальной области определения ничего страшного не произойдёт
 Евгений
Евгений
Но математика это предельный формализм. Если ты занимаешься преобразованием символов, то нельзя так просто забывать об исключительных ситуациях
 Ilya
Ilya
интересно, знал ли уважаемый
Андре́й Никола́евич Колмого́ров (урождённый Катаев, 12 (25) апреля 1903, Тамбов — 20 октября 1987, Москва) — русский советский математик, один из крупнейших математиков ХХ века.
что его классический учебник - для ремесленников?
 Мерль
Мерль
На самом приходится забивать на вот эти все подробности
Например, опускать пределы интегрирования (это самое банальное и забавное, так как часто те же преподаватели, что грешат этим на семинарах, карают за это на проверочных, хыхыхы )
Потому что иначе утонешь в ненужных уточнениях
 Евгений
Евгений
На самом приходится забивать на вот эти все подробности
Например, опускать пределы интегрирования (это самое банальное и забавное, так как часто те же преподаватели, что грешат этим на семинарах, карают за это на проверочных, хыхыхы )
Потому что иначе утонешь в ненужных уточнениях
Ненужных для кого? Для теоретической физики? Да. Для прикладной математики. Возможно. Значительная часть проблем тысячелетия выросла из опущенных ненужных уточнений.
К слову есть разница между "да, мы понимаем, что правильно и корректно писать определённым образом, но я могу напишу по-другому, некорректно, учитывая то, что я могу в уме доказать, что ничего не меняется от этого", и "а, похуй, это у вас определения неправильные"
 Евгений
Евгений
Если использовать Curry-Howard correspondance, то твои ненужные уточнения превратятся в нарушения корректности программы, происходящие с вероятностью ноль
 Мерль
Мерль
Ненужных для кого? Для теоретической физики? Да. Для прикладной математики. Возможно. Значительная часть проблем тысячелетия выросла из опущенных ненужных уточнений.
К слову есть разница между "да, мы понимаем, что правильно и корректно писать определённым образом, но я могу напишу по-другому, некорректно, учитывая то, что я могу в уме доказать, что ничего не меняется от этого", и "а, похуй, это у вас определения неправильные"
Это всё фигня и вот почему:
вопрос состоял в следующем - "Является запись Ильи приемлемой и можно ли ограничиться ею?".
Так как она понятна всем и каждому, как и допущения связанные с нею (например, глядя на неё мы сразу понимаем, какая у функции область определения), то ответ - "да и да".
А вот эти вот экивоки насчёт "бурбаковости", "ереси" и "проблем тысячелетия" - это эстетство на пустом месте и псевдоинтеллигентное наморщивание носика в сторону "нечистых ремесленников", то есть не стоит даже энергии, которую вы затратили на написание сообщений.
Такие делa.
 Евгений
Евгений
Например рассотрим f: R -> R, но f=1/x. Тогда в 0 f не определена, т. е правильно f : R -> Maybe R. И f(0) = Nothing
Эм? Вопрос изначально состоял в том является ли моё замечание о МОЕЙ записи f:R->R, что она не совсем корректна. А кое-кто доебался до меня просто
 Ilya
Ilya
Ну разве что со стороны школьной математики. Со стороны даже обычной университетской правильно f: (-inf, 0) union (0, +inf) -> R
Ну или f: R -> R union {inf}
 Ilya
Ilya
ибо стоило мне начать приводить ссылки (а на готове у меня тупо скрин определения из колмогорова, который я не стал пока кидать), ты заблажил что-то про бурбакизм


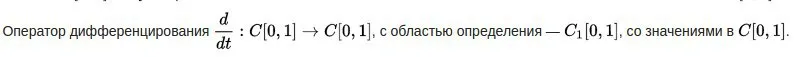
 Нурлан
Нурлан